§1.3 数列极限

一、数列极限

1、数列概念

若按某一法则，对任意自然数 有一个确定的数与之对应，那么，这列有序数

称之为数列，且第 项称之为该数列的一般项。

用函数的观点来看，数列可看作自变量为正整数的函数：

在几何上，数列是数轴上的一个动点。

2、数列极限的语言

【例1】讨论数列 的极限。

数列一般项为 ，观察易知

当 n 愈来愈大，的值愈来愈接近于0，的值愈来愈接近于1。因此，我们可以讲，数列的极限为 1 。

上面的讨论，很大程度上依赖于观察，诸如“愈来愈大”，“愈来愈接近”这类语言也显得含糊不清，因此，我们有必要弄精楚极限的准确数学含义。

在数学上，两个数与之间的接近程度可以用来度量，越小，与就越接近。与1 的接近程度为 。

所谓 “当 n 愈来愈大时，的值愈来愈接近于 1”，意指

当 n 取得足够大时， 可以小于任意给定的正数。

如:给定 ，只要 ，那么数列从第101项起后的一切项

均使不等式 成立。

如:给定 ，只要 ，那么数列从第1001项起后的一切项

均使不等式 成立。

一般地

对于任意给定的充分小正数，总可找到一个正整数，使得对于的一切时的，不等式

总成立。

这就是数列极限的精确数学含义！由此，我们给出数列极限的一般定义：

给定数列，若对于任意给定的正数（无论多么小），总存在一个正整数，当时，不等式

总成立，则称常数是数列的极限，或称收敛于。记作

或（当时）

如果数列无极限，则称数列发散。

在这一定义中，数值是核心，通常也称此定义为语言，用以下符号来加以简述。

,, 当 时，总有

成立，则称数列以为极限，记作。

对极限的精确语言我们给出几点注解:

(1)、正数是任意给定的，因为只有这样不等式才能表达与愈来愈接近的含义，但一经给定就不变了。

(2)、正整数 N 与有关的，一般地讲，越小就越大。但通常 N 的选取不唯一，只要找一个就行了。

(3)、数列极限具有非常明显的几何特征

,, 当 时，有

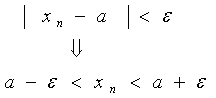
这表明：数列有无限多项 落入区间内，至多只有有限项(至多 N 项)在此区间之外。

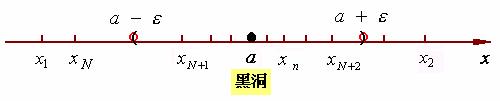
这种现象可以用下图来进行直观解释：

数列有无穷多项凝聚在点的邻域内，点象一个吸力非常大的黑洞，在它的附近吸引了数列中的无穷多项。

(4)、语言只能用来判定数列是否以极限，而不能用它来求数列的极限。

3、用语言证明数列极限举例

【例2】试证明极限

解：，欲使

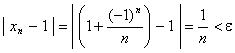
只需，因此可取，当时，有不等式

成立，故 。

【例3】设，试证明等比数列的极限为0。

解：，欲使

只需，即 ( 注意到： )

因此可取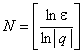，当时，有不等式

成立，故 。

【例4】设，试证明它的极限为0。

二、收敛数列的两个性质

【定理一】(极限的唯一性) 数列 不能收敛于两个不同的极限。

这一定理所陈述的事实显然。据数列极限的几何意义，收敛的数列不可能有两个凝聚点。

【定理二】(收敛数列的有界性) 设数列收敛，则数列一定有界。

若数列收敛于，则它的各项 在数轴上的分布如下图所示

很明显， 数列是有界的。

定理二表明：收敛的数列一定是有界的，那么，有界的数列是否一定收敛呢?

请看一个著名的反例

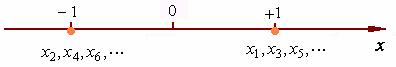
几何上，该数列取值只是-1、+1两点，显然，它们不可能有什么唯一的凝聚点，但它们却是有界的。这表明：有界数列不一定收敛。